首先,必須申明:現實中「穩賺」的機會極少。
這是一個關於「概率、期望值、跨期下注、選擇權、對沖」的嚴謹而有趣的描述。
穩賺需要有具體的前提條件,這些條件非常隱蔽,且經常被忽視。
假如你懂得了「穩賺的機會原理」,就可以反向設計讓自己「穩賺」的那些前提條件,從而獲得對手所不具備的概率優勢。
由此,我將談及「概率權」的把握和主動設計,這些智慧是投資和決策的第一性原理。
本文涉及的計算並不複雜,但真正能夠理解的人也許不到1%。
所以,假如你沒學過概率,沒有決策經驗,從未用自己的錢下過注,就不要輕易懷疑文中計算的正確性。
一、最小回報最大化
讓我們從《普林斯頓概率論讀本》的一道題開始:
有人在拉斯維加斯下了一個賭注,押A球隊能在常規賽中保持不敗,最後贏得冠軍,賠率是1000比1,他下注了500美元,若獲勝將拿走50萬美元。
他運氣不錯,A球隊進入了總決賽,並在比賽中以微弱優勢領先於對手B球隊。這意味着,如果勢頭不變,他的500美元將變成50萬美元。
這時候拉斯維加斯打來電話,說願意用15萬美元買走他的下注。
A、如果他答應,15萬美元馬上到手,但可能失去賺50萬的機會;
B、如果他不答應,就有機會拿走50萬美元,但也可能一分錢都賺不到。
你會選擇哪一個?
上面那位球迷對A球隊很有信心,拒絕了「立即拿走15萬美元」,而是選擇已經快到嘴邊的50萬美元。
這是一個真實的故事。
第四十二屆超級碗,巨人隊(B球隊)在終場前35秒大逆轉,贏了愛國者隊(A球隊)。那位朋友的50萬美元就這樣飛走了。
什麼事情都可能發生。所謂的勝券在握,真的只是一個概率問題。
這位下注者做錯了什麼?
如果我們假設A球隊的獲勝概率大於50%,那麼下注A球隊的期望值也大於(50萬✖️50%=25萬)。該期望值既然大於15萬。所以下注者的選擇「拒絕拉斯維加斯開出的15萬條件」,似乎是對的。
從概率的角度看,有些正確的選擇未必有對的結果。類似於打德撲這類多次博弈,把決策的過程和結果分開看(雖然仍是一個整體),是傳奇女撲克牌手安妮·杜克的關鍵思維模式。
可是,數十萬美金,對誰都不是小數字。而且對於普通球迷來說,用500美元換來這麼大的贏錢機會,一輩子都難得有一次。如果無法多次重複,概率思維還有用嗎?
更不用說還有期望效用和損失厭惡對決策者的影響。
其實,下注者還有另外一種選擇,可以讓他穩贏數十萬美元!
《普林斯頓概率論讀本》的作者米勒教授給出了具體的方法——對沖:
下注者當時可以再下注押B球隊贏。這樣,不管哪一方獲勝,他都可以有可觀的收入。
讓我們來算一下:
假設A球隊的勝率是80%,因為拉斯維加斯要利用賠率差來賺錢,所以假設押注B隊贏的賠率是3。就勝率而言,這是一個對下注者不利的賠率。
這樣一來,這個真實故事中的主角就迎來了一次對沖的機會,他可以反手再下一把注,押B隊贏。如果計算妥當的話,不管是A隊贏,還是B隊贏,下注者都會穩賺。
那麼,他應該下注多少呢?
如上所述,我們設該下注於B隊的金額為B,所以:
1)A隊勝的回報是(50萬-500-B);
2)B隊勝的回報是(B✖️3-500-B)。
由於雙邊下注,我們至少會獲得兩種結果中較小的那個回報,所以接下來我們要追求的是:
令兩種結果中較小的那個數值最大化。
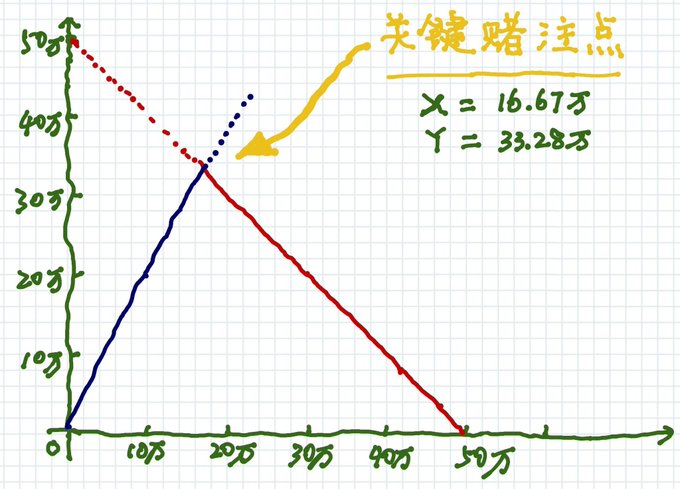
如上圖,橫坐標是B的數值,即下注於B球隊的金額:
紅線是假如A獲勝的回報,表示為:(50萬-500-B)
藍線是假如B獲勝的回報,表示為:(B✖️3-500-B)
縱坐標是A隊勝和B隊勝的不同回報。圖中實線部分,是兩種可能結果中的最小值,如圖可知最小值的最高點是(B✖️3=50萬)。