在平時練習中,掌握簡便算法可以給孩子大大節省時間。今天整理了小學數學簡便算法的匯總大全,各位家長教給孩子,讓孩子數學計算更快更好!
速算順口溜
認識鐘錶
跑的最快是秒針,個兒高高,身材好;
跑的最慢是時針,個兒短短,身材胖。
不高不矮是分針,勻速跑步作用大。
年月日
一三五七八十臘(12月),
三十一天永不差;
四六九冬(11月)三十日;
大月、小月的記憶
七前單月大,
八後雙月大。
運算順序歌
打竹板,響連天,各位同學聽我言,
今天不把別的表,單把四則運算聊一聊,
混合試題要計算,明確順序是關鍵。
同級運算最好辦,從左到右依次算,
兩級運算都出現,先算乘除後加減。
遇到括號怎麼辦,小括號里算在先,
中括號里後邊算,次序千萬不能亂,
每算一步都檢查,又對又快喜心間。
"除"的意義
看到"除",圈一圈,
"除"字前面是除數,
"除"字後面被除數,
位置交換別忘了。
多位數讀法歌
讀數要從高位起,哪位是幾就讀幾,
每級末尾若有零,不必讀出記心裏,
其他數位連續零,只讀一個就可以,
萬級末尾加讀萬,億級末尾加讀億。
多位數寫法歌
寫數要從高位起,哪位是幾就寫幾,
哪一位上沒單位,用0佔位要牢記。
多位數大小比較歌
位數不同比大小,
位數多的大,位數少的小,
位數相同比大小,
高位比起就知道。
100以內的質數口訣
2、3、5、7和11,
13後面是17,
19、23、29,(十九、二三、二十九)
31、37、41,(三一、三七、四十一)
43、47、53,(四三、四七、五十三)
59、61、67,(五九、六一、六十七)
71、73、79,(七一、七三、七十九)
83、89、97。(八三、八九、九十七)
商中間或末尾有0的除法
我是0,本事大,
除法運算顯神通。
不夠商1我來補,
有了空位我就坐。
別人要想把我除,
常勝將軍總是我。
20以內進位加法
看大數,分小數,湊整十,加零頭。
(掌握「湊十法」,提倡「遞推法」。)
20以內退位減法
20以內退位減,口算方法和簡單。
十位退一,個加補,又准又快寫得數。
加法意義,豎式計算
兩數合併用加法,加的結果叫做和。
數位對其從右起,逢十進一別忘記。
減法的意義豎式計算
從大去小用減法,減的結果叫做差。
數位對齊從右起,不夠減時前位拿。
兩位數乘法
兩位數乘法並不難,計算過程有三點:
乘數個位要先算,再用十位乘一遍,
乘積末位是關鍵,要和十位來對端;
兩次乘積相加完,層層計算記心間
兩位數除法
除數兩位看兩位,兩位不夠除三位。
除到那位商那位,餘數要比除數小,
然後再除下一位,試商方法要靈活,
掌握「四捨五入」法,還有「同商比較法」,
了解「折半定商法」,不足除數商九、八。
(包括:同頭、高位少1)
混合運算
拿到式題認真看,先算乘除後加鹼。
遇到括號要先算,運用規律要改變。
一些數據要記牢,技能技巧掌握好。
加、減法速算
加減法速算你莫愁,拿到算式看清楚,
接近整百湊整數,如下處理無謬誤。
加法不足減補數,超餘零頭加在後。
減法不足加補數,超餘零頭減在後。
多位數讀法
讀書方法很容易,首先四位一分級。
要從最高位讀起,幾千幾百幾十幾。
級的單位讀億萬,末尾有零都不讀
(級末尾0不讀,整個數末尾0不讀)
中間夾零讀一個,漢字表達沒參和。
讀零的
萬級個級首位有零;
整個萬級是零;
上級末尾下級首位都有0;
每級中間有0。
小數加減法
小數加減計算題,以點對準好對齊。
算法如同算整數,算畢把點往下移。
小數乘法
小數乘小數,法則同整數。
定積小數位,因數共同湊。
除數是小數的除法
除數的小數點一划,(去掉小數點)
被除數的小數點搬家,向右搬家搬幾位,
除數的小數位數決定它。
四捨五入法兒歌
四捨五入方法好,近似數來有法找;
取到哪位看下位,再同5字作比較;
是5大5前進1,小於5的全舍掉;
等號換成約等號,使人一看就明了。
除數是一位數的除法
除數一位看一位,一位不夠看兩位,(一看)
除到哪位商那位,(二商三乘減)
除數是兩位的除法
除數兩位看兩位,兩位不夠看三位。
除到哪位商那位,記熟口訣定好位。
試商方法要靈活,不夠商「1」「0」佔位。
餘數要比除數小,然後再除下一位。
除數當姐余當妹。(四比五餘)
四則混合運算的運算順序
括號括號搶第一,
乘法、除法排第二,
最後才算加減法,
誰在前面先算誰。
質數歌
一位質數2、3、5和7,
兩位1、3、7、9前加1,
4後3,7前有9,7後1,
3、4、6後加7、1,
2、5、7、8後添9、3,
二十五個質數要記全。
分數乘除法
分數乘法易學懂,分子分母分別乘。
算式意義要搞清,上下能約更輕鬆。
分數除法方法妙,原來除號變乘號。
除數子母打顛倒,進行計算離不了。
約分
約分、約分,相乘約淨,省時省力。
從上往下,從左到右,弄清數據,一數不漏。
遇到小數,去點為整,位數不夠,用「零」來補。
互質數的判斷
分數比化簡,互質數兩端。
觀察記五點:1和所有數;
相鄰兩個數;兩質必互質。
大數是質數,兩數定互質。
小數是質數,大數不倍數。(是小數的)
文字題
敘述形式有三種,讀法意義和名稱。
解題方法要記清,縮句化簡一步算。
標點詞語把句斷,分層布列莫遲延。
列式方法有兩種,可用算式和方程。
比較關係應用題
(一)相差關係
多多少,少多少,都是大減小。
已知條件說比多,比前用加比後減。
已知條件說比少,比前用減比後加。
(二)倍數關係
倍在問題里用除。
倍在已知條件里,
求是前用乘,求是後用除。
(三)求比幾倍多(少)幾的數
根據倍數分乘數,根據多少分加減。
算除先加減,算乘後加減。
找單位「1」
單位「1「藏得巧,根據分率把你找。
「其中「的前站得好,」是、占、比「後坐得妙;
「問答式「能找到,補充說明要搞好。
百分數常遇到,不帶「率「字有禮貌。
找出一對好朋友,然後確定乘除號。
找單位「1「的說明:
抓住含有不帶單位名稱的分數的「關鍵句「、「關鍵詞」,進行剖析,這樣就解決了不少學生對於分數應用題苦於不知「從何下手」進行分析數量關係。因此,使學生學會迅速找「關鍵句」、「關鍵詞語」進行剖析數量關係,不僅能有利於掌握解答分數應用題的一般規律,而且也能培養學生的能力,發展學生的智力。先「找」後「析」是六年級學生普遍的學習規律,切記引導學生認真有序地進行分析。
正反比例應用題
正比例,分三段,不變數量在中間,
前後歸一分開列,然後等號來連接。
反比例分三段,不變數量在前面,
「如果」分開歸總列,再用等號來連接。
速算技巧
低年級組
1.加數「湊整」
幾個數相加,如果有幾個數相加能湊成整十的數,可以調換加數的位置,把幾個數相加。
例:14+5+6
=14+6+5
=25
2.運用減法性質「湊整」
從一個數里連續減去幾個數,如果減數的和能湊成整十的數,可以把減數先加後再減。這種口算比較簡便。
例:50-13-7
=50-(13+7)
=50-20
=30
3.近十、近百、近千的數
計算時可以把接近整十、整百、整千……的數看作整十、整百、整千……的數進行解答。
例:
1)497+136
497可以近似的看成500,
原式=(500-3)+136
=500+136-3
=633
2)760+102
將102看成100+2
原式=760+100+2
=860+2
=862
4.補數法
利用「補數法」,將每個加數加1後湊成20000、2000、200、20進行計算。
例:19999+1999+199+19
可以看成:
(20000-1)+(2000-1)+(200-1)+(20-1)
=20000+2000+200+20-4
=22220-4
=22216
5.利用加減法交換律:
先加再減的題目也可以做成先減再加。
例:562+316-62
=562-62+316
=500+316
=816
6.整百數和「零頭數」
在計算時可以先把題中的數看成兩部分:整百數和「零頭數」,然後把整百數與整百數相加減,「零頭數」與「零頭數」相加減。
例:598+31-296-103
=500+98+31-200-96-100-3
=500-200-100+98-96+31-3
=200+2+28
=230
中年級組
1.帶符號搬家法
當一個計算題只有同一級運算(只有乘除或只有加減運算)又沒有括號時,我們可以「帶符號搬家」。
例如:
23-11+7=23+7-11
4×14×5=4×5×14
10÷8×4=10×4÷8
2.結合律法
加括號法
(1)在加減運算中添括號時,括號前是加號,括號里不變號,括號前是減號,括號里要變號。
例如:
23+19-9=23+(19-9)
33-6-4=33-(6+4)
(2)在乘除運算中添括號時,括號前是乘號,括號里不變號,括號前是除號,括號里要變號。
例如:
2×6÷3=2×(6÷3)
10÷2÷5=10÷(2×5)
去括號法
(1)在加減運算中去括號時,括號前是加號,去掉括號不變號,括號前是減號,去掉括號要變號(原來括號里的加,現在要變為減;原來是減,現在就要變為加)。
例如:
17+(13-7)=17+13-7
23-(13-9)=23-13+9
23-(13+5)=23-13-5
(2)在乘除運算中去括號時,括號前是乘號,去掉括號不變號,括號前是除號,去掉括號要變號(原來括號里的乘,現在就要變為除;原來是除,現在就要變為乘。)
例如:
1×(6÷2)=1×6÷2
24÷(3×2)=24÷3÷2
24÷(6÷3)=24÷6×3
3.乘法分配律法
分配法
括號里是加或減運算,與另一個數相乘,注意分配。
例如:
8×(5+11)=8×5+8×11
提取公因式法
注意相同因數的提取。
例如:
9×8+9×2=9×(8+2)
4.湊整法
看到名字,就知道這個方法的含義。用此方法時,需要注意觀察,發現規律。還要注意還哦,有借有還,再借不難嘛。
例如:
99+9=(100-1)+(10-1)
5.方法五:拆分法
拆分法就是為了方便計算,把一個數拆成幾個數。這需要掌握一些「好朋友」,如:2和5,4和5,4和25,8和125等。分拆還要注意不要改變數的大小哦。
例如:
32×125×25
=4×8×125×25
=(4×25)×(8×125)
=100×1000
高年級組
1.速算之湊整先算
【點撥】:加法、減法的簡便計算中,基本思路是「湊整」,根據加法(乘法)的交換律、結合律以及減法的性質,其中若有能夠湊整的,可以變更算式,使能湊整的數結成一對好朋友,進行湊整計算,能使計算簡便。
例:298+304+196+502
【分析】:本題可以運用加法交換律和結合律,把能夠湊成整十、整百、整千……的數先加起來,可以使計算簡便。
【解答】:原式=(298+502)+(304+196)=800+500=1300
2.速算之帶符號搬家
【點撥】:在加減混合,乘除混合同級運算中,可以根據運算的需要以及題目的特點,交換數字的位置,可以使計算變得簡便。特別提醒的是:交換數字的位置,要注意運算符號也隨之換位置。
例:464-545+836-455
【分析】:觀察例題我們會發現,如果按照慣例應該從左往右計算,464減545根本就不夠減,在小學階段,學生沒辦法做,所以要想做這道題,學生必須先觀察數字特點,進行簡便計算。
思考:4.75÷0.25-4.75能帶符號搬家嗎?什麼情況下才能帶符號搬家?帶符號搬家需要注意什麼?
3.速算之拆數湊整
【點撥】:根據運算定律和數字特點,常常靈活地把算式中的數拆分,重新組合,分別湊成整十、整百、整千。
例:998+1413+9989
【分析】:給998添上2能湊成1000,給9989添上11湊成10000,所以就把1413分成1400、2與11三個數的和。
【解答】:原式==(998+2)+1400+(11+9989)=1000+1400+10000=12400
例:73.15×9.9
【分析】:把9.9看作10減0.1的差,然後用乘法分配率可簡化運算。
【解答】:原式=73.15×(10-0.1)=73.15×10-73.15×0.1=731.5-7.315=724.185
4.速算之等值變化
【點撥】:等值變化是小學數學中重要的思想方法。做加法時候,常常利用這樣的恆等變形:一個加數增加,另一個加數就要減少同一個數,它們的和才不變。而減法中,是被減數和減數同時增加或減少相同的數,差才不變。
例:1234-798
【分析】:把798看作800,減去800後,再在所得差里加上多減去的2.
【解答】:原式==1234-800+2=436。
5.速算之去括號法
【點撥】:在加減混合運算中,括號前面是「加號或乘號」,則去括號時,括號里的運算符號不變;如果括號前面是「減號或除號」,則去括號時,括號里的運算符號都要改變。
例題:(4.8×7.5×8.1)÷(2.4×2.5×2.7)
【分析】:首先根據「去括號原則」把括號去掉,然後根據「在同級運算中每個數可帶着它前邊的符號『搬家』」進行簡算。
【解答】:原式=4.8×7.5×8.1÷2.4÷2.5÷2.7
=(4.8÷2.4)×(7.5÷2.5)×(8.1÷2.7)
=2×3×3
=18
6.速算之同尾先減
【點撥】:在減法計算時,若減數和被減數的尾數相同,先用被減數減去尾數相同的減數,能使計算簡便。
【分析】:算式中第二個減數256與被減數2356的尾數相同,可以交換兩個數的位置,讓2356先減256
7.速算之提取公因數
【點撥】:乘法分配率的反應用,出錯率比較高,一般包括三種類型。
(1)直接提取
例3.65×23+3.65×77
【分析】:這道題比較簡單,利用乘法分配律的反向應用,直接提取公因數3.65就行了。
【解答】:原式=3.65×(23+77)=3.65×100=365
(2)省略×1的題目
例:6.3×101-6.3
【分析】:把算式補充完整,6.3×101-6.3×1,學生就很容易看出兩個乘法算式中有相同的因數6.3
【解答】:原式=6.3×(101-1)=6.3×100=630
(3)積不變規律(主要是小數點的變化)
例:6.3×2.57+25.7×0.37
【分析】:可根據「乘法積不變性質,一個因數擴大,一個因數縮小相同的倍數,積不變」把25.7×0.37轉化成2.57×3.7,兩部分就有了相同的因數2.57,創造出了可以用乘法分配律的條件。
【解答】:原式=6.3×2.57+2.57×3.7=2.57×(6.3+3.7)=25.7
特殊數的速算技巧
1.不管是幾個1的平方,都是有規律的。

2.乘數固定為8,加數遞增,就會變成有規律的金字塔型。

3.不管是什麼樣的二位數乘以11,乘積的百位和個位數字會是被乘數的兩個數字,而十位數字則是被乘數的數字相加。

4.若乘數是11,不管被乘數是多少,只要把頭尾數字寫好,中間的數字按照下圖相加,就能輕鬆得出答案。
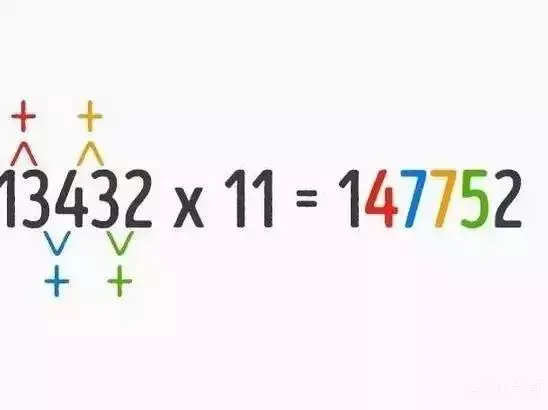
5.九九乘法表裏,9x3=27,9x8=72,乘積剛好是顛倒的數字!只有9的乘積是這樣。

6.被乘數為9的乘積是有規律的。

7.面對數字超大的平方數,可以按照下面的公式計算。不過只有靠近100的平方數比較好算。

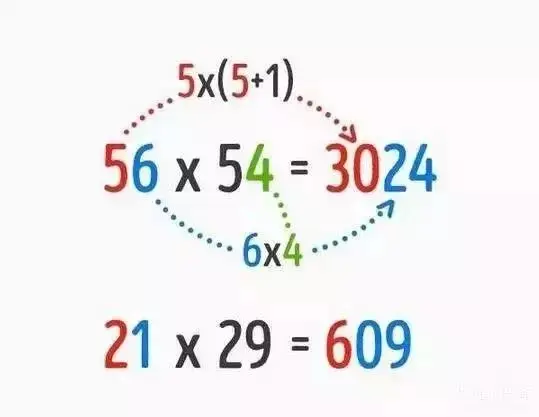
8.分子為一,分母不同的數字相加時,只要找出分母的最小公倍數,把分母變成一樣的數字就可以了。
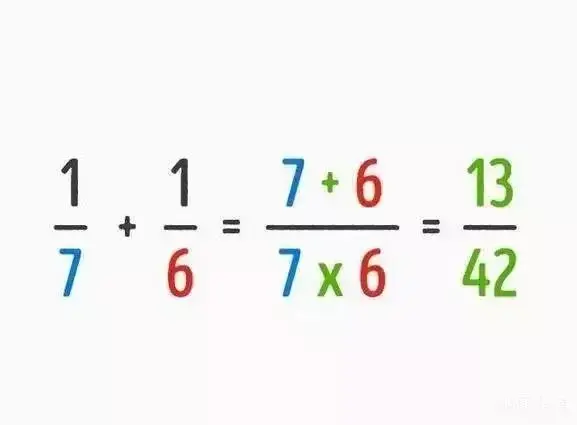
9.被乘數和乘數都很大的話,把被乘數十位數以上的數字以下面的公式運算:十位數以上x(十位數以上+1)為乘積的「頭」,被乘積與乘積的個位數字互乘為「尾」,就能算出答案,不過尾數要相加等於10才行。